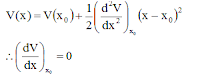One Dimensional Oscillator (small oscillations)

• Consider a system with one degree of freedom and one generalized co-ordinate q. For small displacement from the equilibrium we can expand potential energy function using taylor series expansion about the equilibrium and we will only consider the lowest order terms. So expanding PE function V(q) we have
  
  
  
  
  
  
  where derivativesare evaluated at the equilibrium position q=q₀ and at equlilbrium (∂V/∂q)₀ = 0
• V(q₀) is potential energy at equilibrium and can be taken as zero, if the origin of potential energy is shifted to be at minimum equilibrium value.
  This implies that
  
  
  
  
  
  
  
  
  putting second derivative term in bracket equal to k and shifting origin to q₀=0 we have
  V(q)=kq²/2
  and k is the positive parameter at the position of stable equilibrium.
• If generalized co-ordinates does not involve time explicitely , the K.E. is then homogeneous quadratic function of generalized velocities, or,.
  
  

where coefficent m(q) , is in general function of q co-ordinate and may also be expanded in taylor series about the equilibrium position as we have done for potential energy function and first derivative of q is quadratic in this equation and the lowest lowest nonvanishing approximation to T is obtained by retaining only the firt term in the Taylor series expansion of m(q) which is m(0). Thus Lagrangian for small oscillations of one dimensional oscillator is

and equation of motion is

Stable and unstable equilibrium

First consider the figures given below

• Above are the plots of potential energy as a function of x , for a particle executing bound and unbound motion.
• At x₀=0 slope of potential energy curve dV/dx is zero. this implies that F = 0 i.e.,
          F = -dV/dx = 0                 (1)
  and a point particle placed at such a point with zero velocity will continue to remain at rest.
• At point x₀ in figugure (a) at which potential energy has a minimum , if the particle is displaced then the force F = -dV/dx will tend to return to it and it will oscillate about the equilibrium point, performing bound motion. These points are called points of stable equilibrium.
• If the particle is displaced slightly from the equilibrium x₀ in figure (b) , then it will be acted upon by the force
        F(x) = -(-dV/dx) = dV/dx          (2)
  which will tend to push away the particle from equilibrium point , when released. Such points are called points of unstable equilibrium.

Potential energy about point of stable equilibrium
Suppose the particle is slightly displaced from point of stable equilibrium executing small oscillations then potential energy function can be expressed in the form of Taylor - series expansion i.e.,