- Above are the plots of potential energy as a function of x , for a particle executing bound and unbound motion.
- At x0=0 slope of potential energy curve dV/dx is zero. this implies that F = 0 i.e.,
F = -dV/dx = 0 (1)
and a point particle placed at such a point with zero velocity will continue to remain at rest. - At point x0 in figugure (a) at which potential energy has a minimum , if the particle is displaced then the force F = -dV/dx will tend to return to it and it will oscillate about the equilibrium point, performing bound motion. These points are called points of stable equilibrium.
- If the particle is displaced slightly from the equilibrium x0 in figure (b) , then it will be acted upon by the force
F(x) = -(-dV/dx) = dV/dx (2)
which will tend to push away the particle from equilibrium point , when released. Such points are called points of unstable equilibrium.
Potential energy about point of stable equilibrium
Suppose the particle is slightly displaced from point of stable equilibrium executing small oscillations then potential energy function can be expressed in the form of Taylor - series expansion i.e.,

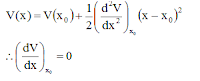
No comments:
Post a Comment