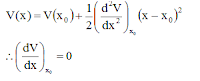Total energy of earth in its circular orbit around the sun

Question :
Find out the total energy of earth in its circular orbit around the sun in terms of gravitational constant
Answer:
Let R be the total distance between the earth and the sun. If \({M_e}\) and \({M_s}\) are the mass of earth and sun respectively, the gravitational force of motion of earth and sun is given by

\(F =  - \frac{{G{M_e}{M_s}}}{{{R^2}}}\)

where G is the gravitational constant. Since the centripetal force balances the gravitational force of attraction, we have

\({F_c} = |{F_G}|\),

where

\({F_c} = \frac{{{M_e}{v^2}}}{R}\)

v being the velocity with which earth is moving. Hence we have

\(\frac{{{M_e}{v^2}}}{R} = \frac{{G{M_e}{M_s}}}{{{R^2}}}\)

or

\({M_e}{v^2} = \frac{{G{M_e}{M_s}}}{R}\)

Therefore kinetic energy of earth in motion is

\(T = \frac{1}{2}{M_e}{v^2} = \frac{1}{2}\frac{{G{M_e}{M_s}}}{R}\)

As we know that , force in terms of potential energy is

\({F_G} = - \frac{{\partial V}}{{\partial R}}\)
\(V = - \int {{F_G}dR} = \int {\frac{{G{M_e}{M_s}}}{{{R^2}}}dR = - } \frac{{G{M_e}{M_s}}}{R}\)

Now total energy of the earth in the orbit around the sun is

\(E = T + V\)
\(E = \frac{1}{2}\frac{{G{M_e}{M_s}}}{R} - \frac{{G{M_e}{M_s}}}{R}\)

\(E = - \frac{1}{2}\frac{{G{M_e}{M_s}}}{R}\)

This is the required expression.

Brachistochrone Problem

Question

If a particle falls from rest under the influence of gravity from higher to lower point in the minimum time, what is the curve that the particle will follow?

Solution

Suppose v is the speed of the particle along the curve, then in traversing ds portion of the curve time spent would be \(\frac{{ds}}{v}\) so that total time taken by the particle in moving from highest point 1 to lowest point 2 will be

\[{t_{12}} = \int\limits_1^2 {\frac{{ds}}{v}} \]

Suppose vertical distance of fall upto point 2 be x, then from the principle of conservation of energy of the particle we find that

\(\begin{array}{l}\frac{1}{2}m{v^2} = mgx\\or\\v = \sqrt {2gx} \\then\\{t_{12}} = \int\limits_1^2 {\frac{{\sqrt {d{x^2} + d{y^2}} }}{{\sqrt {2gx} }}} dx\\{\rm{      = }}\int\limits_1^2 {\frac{{\sqrt {1 + {{\dot y}^2}} }}{{\sqrt {2gx} }}} dx\\{\rm{      = }}\int\limits_1^2 {fdx} \end{array}\)

Where,

\( f=\left ( \frac{1+\dot{y}^{2}}{2gx} \right )^{\frac{1}{2}} \)

For \({t_{12}}\) to be minimum equation

\(\frac{d}{{dx}}\left( {\frac{{\partial f}}{{\partial \dot y}}} \right) - \frac{{\partial f}}{{\partial y}} = 0\)

must be satisfied. From expression for \(f\) we find that

\(\begin{array}{l}\frac{{\partial f}}{{\partial y}} = 0\\\frac{{\partial f}}{{\partial \dot y}} = \frac{{\dot y}}{{\sqrt {2gx} \sqrt {1 + {{\dot y}^2}} }}\\\frac{d}{{dx}}\left( {\frac{{\dot y}}{{\sqrt {2gx} \sqrt {1 + {{\dot y}^2}} }}} \right) = 0\\or\\\frac{{{{\dot y}^2}}}{{2gx(1 + {{\dot y}^2})}} = c'\end{array}\)

Where c’ is the constant of integration.

Since c’ is a constant we can also write

\(\frac{{{{\dot y}^2}}}{{x(1 + {{\dot y}^2})}} = c\)

where c is also a constant. On integrating above equation we find

\(\begin{array}{l}\frac{{{{\dot y}^2}}}{c} = x(1 + {{\dot y}^2})\\or,\\{{\dot y}^2}\left( {\frac{1}{c} - x} \right) = x\\{{\dot y}^2}\left( {\frac{x}{c} - {x^2}} \right) = {x^2}\\\dot y = \frac{x}{{\sqrt {\frac{x}{c} - {x^2}} }}\end{array}\)

Putting \(\frac{1}{c} = 2a\) , and on integration we get

\(\int dy=\int \frac{x}{\sqrt{2ax-x^{2}}}dx\)

\( y=acos^{-1}(1-\frac{x}{a})-(2ax-x^{2})^{1/2}+c''\)

where c'' is new constant of integration.
In case c'' is zero then y will be zero for x=0.

As such the equation

\( y=acos^{-1}(1-\frac{x}{a})-(2ax-x^{2})^{1/2}\)

And this y represents an inverted cycloid with its base along y axis and cusp at the origin and is the curve that particle will follow.

Double pendulum

Question 

In case of a double pendulum find the expression for the kinetic energy of the system

Solution

We take a simple case where lengths and masses are same.see below in the figure

Here on being displaced the co-ordinates of two pendulums are

\(\begin{array}{l}{x_1} = l\sin {\theta _1}\\{y_1} = l\cos {\theta _1}\end{array}\)

For the first pendulum where \({\theta _1}\) is the angle through which the first pendulum have been displaced.

For second pendulum

\(\begin{array}{l}{x_2} = l\sin {\theta _1} + l\sin {\theta _2}\\{y_2} = l\cos {\theta _1} + l\cos {\theta _2}\end{array}\)

Where \({\theta _2}\) is the angle through which second pendulum has been displaced.

The total kinetic energy of the system is given by the expression

\(T = \frac{1}{2}m(\dot x_1^2 + \dot y_1^2) + \frac{1}{2}m(\dot x_2^2 + \dot y_2^2)\)

Now

And

Which is the required result

How to Find Kinetic energy in terms of spherical co-ordinates

Question

How to Find Kinetic energy in terms of \((r,\theta ,\phi )\)

Solution

We have to find the kinetic energy in terms of \((r,\theta ,\phi )\) that is in terms of spherical c0-ordinates. Kinetic energy in terms of Cartesian co-ordinates is

\(T = \frac{1}{2}m\left( {{{\dot x}^2} + {{\dot y}^2} + {{\dot z}^2}} \right)\)                                                                (1)

Where \(\dot x,\dot y{\rm{ and }}\dot z\) are derivatives of z, y and z with respect to time.

Cartesian co-ordinates x, y, z in terms of \(r,\theta \) and \(\phi \) are

\(\begin{array}{l}x = r\sin \theta \cos \phi \\y = r\sin \theta \sin \phi \\z = r\cos \theta \end{array}\)

Now derivatives of x, y and z w.r.t. t are

\(\begin{array}{l}\dot x = \frac{{dx}}{{dt}} = \dot r\sin \theta \cos \phi  + r\cos \theta \cos \phi \dot \theta  - r\sin \theta \sin \phi \dot \phi \\\dot y = \frac{{dy}}{{dt}} = \dot r\sin \theta \sin \phi  + r\cos \theta \sin \phi \dot \theta  + r\sin \theta \cos \phi \dot \phi \\\dot z = \frac{{dz}}{{dt}} = \dot r\cos \theta  - r\sin \theta \dot \theta \end{array}\)  

Where

\(\dot r = \frac{{dr}}{{dt}},\dot \theta  = \frac{{d\theta }}{{dt}},\dot \phi  = \frac{{d\phi }}{{dt}}\)  means all \(r,\theta \) and \(\phi \) changes with time as the particle moves or changes its position with time.

Now calculate for \({\dot x^2},{\dot y^2},{\dot z^2}\) and add them. After adding them we get

\({(\dot x)^2} + {(\dot y)^2} + {(\dot z)^2} = {\dot r^2} + {r^2}{\dot \theta ^2} + {r^2}{\sin ^2}\theta {\dot \phi ^2}\)

Putting this value of \({(\dot x)^2} + {(\dot y)^2} + {(\dot z)^2}\)in equation 1 we get kinetic energy of particle or system in terms of \(r,\theta \) and \(\phi \).

Hence

\(T = \frac{1}{2}m({\dot r^2} + {r^2}{\dot \theta ^2} + {r^2}{\sin ^2}\theta {\dot \phi ^2})\)

Equations of motion of coupled pendulum using the lagrangian method

Question

Obtain the equations of motion of coupled pendulum using the lagrangian method.

Solution

Consider a system of coupled pendulums as shown below in the figure

The displacement of A is \({x_1}\) and B is\({x_2}\) , condition being \({x_1}\) < \({x_2}\). In such state the spring gets stretched. The lengths of the strings of both the pendulums are same (say l). The angular displacement of A is \({\theta _1}\) and that of B is \({\theta _2}({\theta _2} > {\theta _1})\).

Therefore

\(\begin{array}{l}{x_1} = l{\theta _1} \Rightarrow {\theta _1} = \frac{{{x_1}}}{l}{\rm{                      (1)}}\\{x_2} = l{\theta _2} \Rightarrow {\theta _2} = \frac{{{x_2}}}{l}{\rm{                     (2)}}\end{array}\)

As the spring gets stretched, it is clear from the figure that restoring force works along the direction of displacement \({\theta _1}\) and opposite to the direction of displacement\({\theta _2}\) . Now A and B at zero potential level, the total potential energy of the system is given as

\(V = mgl(1 - \cos {\theta _1}) + mgl(1 - \cos {\theta _2}) + \frac{1}{2}k{({x_2} - {x_1})^2}\)

Where m is the mass of each one of the bob and k is the spring constant.

Since \({\theta _1}\)and \({\theta _2}\)are small so,

\(\begin{array}{l}\cos {\theta _1} = 1 - \frac{{\theta _1^2}}{2} + \frac{{\theta _1^4}}{4} + ......\\\cos {\theta _2} = 1 - \frac{{\theta _2^2}}{2} + \frac{{\theta _2^4}}{4} + ......\end{array}\)

Neglecting the higher powers other than squares of \({\theta _1}\)and \({\theta _2}\)the expression of potential energy can be written as

\(\begin{array}{l}V = mgl\frac{{\theta _1^2}}{2} + mgl\frac{{\theta _2^2}}{2} + \frac{1}{2}k{({x_2} - {x_1})^2}\\{\rm{    = }}\frac{{mgx_1^2}}{{2l}} + \frac{{mgx_2^2}}{{2l}} + \frac{1}{2}k{({x_2} - {x_1})^2}\end{array}\)

Also the kinetic energy of whole system is

\(T = \frac{1}{2}m\dot x_1^2 + \frac{1}{2}m\dot x_2^2 = \frac{1}{2}m(\dot x_1^2 + \dot x_2^2)\)

Hence Lagrangian L would be

\(\begin{array}{l}L = T - V\\L = \frac{1}{2}m(\dot x_1^2 + \dot x_2^2) - \frac{{mgx_1^2}}{{2l}} - \frac{{mgx_2^2}}{{2l}} - \frac{1}{2}k{({x_2} - {x_1})^2}\end{array}\)

Now

 \(\begin{array}{l}  \frac{\partial L}{\partial {{x}_{1}}}=-\frac{mg{{x}_{1}}}{l}+k({{x}_{2}}-{{x}_{1}}) \\\end{array}\)

\(\begin{array}{l}\frac{\partial L}{\partial {{{\dot{x}}}_{1}}}=m{{{\dot{x}}}_{1}} \\\end{array}\)

\(\begin{array}{l}\therefore \frac{d}{dt}\left( \frac{\partial L}{\partial {{{\dot{x}}}_{1}}} \right)=\frac{d}{dt}(m{{{\dot{x}}}_{1}})=m{{{\ddot{x}}}_{1}} \\\end{array}\)

Hence Lagrangian equation in terms of \({x_1}\)is

\(\begin{array}{l}\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{\dot x}_1}}}} \right) - \frac{{\partial L}}{{\partial {x_1}}} = 0\\or,\\m{{\ddot x}_1} + \frac{{mg{x_1}}}{l} - k({x_2} - {x_1}) = 0\\or,\\m{{\ddot x}_1} =  - \frac{{mg{x_1}}}{l} + k({x_2} - {x_1})\end{array}\)

Also,

\(\begin{array}{l}\frac{{\partial L}}{{\partial {x_2}}} =  - \frac{{mg{x_2}}}{l} - k({x_2} - {x_1})\\\frac{{\partial L}}{{\partial {{\dot x}_2}}} = m{{\dot x}_2}\\and\\\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{\dot x}_2}}}} \right) = m{{\ddot x}_2}\end{array}\)

Hence Lagrangian equation in terms of \({x_2}\)is

\(\begin{array}{l}\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{\dot x}_2}}}} \right) - \frac{{\partial L}}{{\partial {x_2}}} = 0\\or,\\m{{\ddot x}_2} =  - \frac{{mg{x_2}}}{l} - k({x_2} - {x_1})\end{array}\)

The equation of motion for given system are

\(\begin{array}{l}m{{\ddot x}_1} =  - \frac{{mg{x_1}}}{l} + k({x_2} - {x_1})\\m{{\ddot x}_2} =  - \frac{{mg{x_2}}}{l} - k({x_2} - {x_1})\end{array}\)

Lagrangian problem

Question The Lagrangian for a mechanical system is $L=a\dot q^2+bq^4$ where $q$ is a generalized coordinate and $a$ and $b$ are constants. The equation of motion for this system is
A. $\dot q=\sqrt{\frac{b}{a}}q^2$
B. $\dot q=\frac{2b}{a} q^3$
C. $\ddot q=\frac{-2b}{a} q^3$
D. $\ddot q=+\frac{2b}{a} q^3$
E. $\ddot q=\frac{b}{a} q^3$
Solution:
The Lagrangian equation of motion for the generalized coordinate $q$:
$\frac{\partial L}{\partial q}=\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot q}$
$\frac{\partial L}{\partial q}=\frac{\partial}{\partial q} (a\dot q^2+bq^4 )=0+\frac{\partial}{\partial q} bq^4=4bq^3$
$\frac{\partial L}{\partial \dot q}=\frac{\partial}{\partial \dot q} (a\dot q^2+bq^4 )=\frac{\partial}{\partial \dot q} a\dot q^2+0=2a\dot q$
$\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot q}=\frac{\partial}{\partial t} 2a\dot q=2a \ddot q$
$\frac{\partial L}{\partial q}=\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot q} \rightarrow 4bq^3=2a\ddot q \rightarrow \ddot q=\frac{2b}{a} q^3$
source :-http://physics-problems-solutions.blogspot.com

What are constraints

Sometimes motion of a particle or system of particles is restricted by one or more conditions. The limitations on the motion of the system are called constraints. The number of co-ordinates needed to specify the dynamical system becomes smaller when constraints are present in the system. Hence the degree of freedom of a dynamical system is defined as the minimum number of independent co-ordinates required to simplify the system completely along with the constraints. Thus if k is the number of constraints and N is the number of particles in the system possessing motion in three dimensions then the number of degrees of freedom are given by
n=3N-k                                  (1)
thus the above system has n degrees of freedom.
Constraints may be classified in many ways. If the condition of constraints can be expressed as equations connecting the co-ordinates of the particles and possibly the time having the form
f(r₁,r₂,......t)=0                          (2)
then constraints are said to be holonoic and the simplest example of holonomic constraints is rigid body. In case of rigid body motion the distance between any two particles of the body remains fixed and do not change with the tie. If r_i and r_j are the position vectors of the i'th and j'th particles then , the distance between the is given by
|r_i-r_j|=c_ij                                   (3)
The constraints which are not expressible in the form of equation 2 are called non-holonoic for example, the motion of a particle placed on the surface of a sphere of radius a will be described as
|r|≥a or, r-a≥0
Constraints can further be described as (i) rehonoic and(ii) scleronoous. In rehonomous constraints the equation of constraints contains time as explicit variable while in case of scleronomous constraints they are not explicitly dependent on time.

What are Legendre transformations

The transition from Lagrangian to Hamiltonian formulism corresponds to changing the variables in our mechanical functions from $(q,\stackrel{}{\stackrel{.}{q}},t)\stackrel{}{\mathrm{to}(q,p,t)}$

where , p is related to q and $\stackrel{.}{q}$ by the equation

$p_i=\frac{\partial L(q_j,{\dot{q}}_j,t)\stackrel{}{{}_{}}}{\partial {\dot{q}}_i}$

The procedures for switching variables in this manner is provided by the legendre transformations.

Consider a function of only two variables f(x,y), so that differential of f has the form

df=udx+vdy

where , $u=\frac{\mathrm{df}}{\mathrm{dx}}$ and $v=\frac{\mathrm{df}}{\mathrm{dy}}$                      (1)

To change the basis of description from x,y to a new set of variables u,y , so that differential quantities are expressed in terms of differential du and dy. Let g be the function of u and y defined by the equation

g=f-ux

differential of g is given as

dg=df-udx-xdu

or,

dg=vdy-xdu

which is exactly in the desired form. The quantities x and v are now functions of variables u and y given by the relations

$x=-\frac{\partial g}{\partial u},v=\frac{\partial g}{\partial y}$

which are exactly converse of equation 1

One Dimensional Oscillator (small oscillations)

• Consider a system with one degree of freedom and one generalized co-ordinate q. For small displacement from the equilibrium we can expand potential energy function using taylor series expansion about the equilibrium and we will only consider the lowest order terms. So expanding PE function V(q) we have
  
  
  
  
  
  
  where derivativesare evaluated at the equilibrium position q=q₀ and at equlilbrium (∂V/∂q)₀ = 0
• V(q₀) is potential energy at equilibrium and can be taken as zero, if the origin of potential energy is shifted to be at minimum equilibrium value.
  This implies that
  
  
  
  
  
  
  
  
  putting second derivative term in bracket equal to k and shifting origin to q₀=0 we have
  V(q)=kq²/2
  and k is the positive parameter at the position of stable equilibrium.
• If generalized co-ordinates does not involve time explicitely , the K.E. is then homogeneous quadratic function of generalized velocities, or,.
  
  

where coefficent m(q) , is in general function of q co-ordinate and may also be expanded in taylor series about the equilibrium position as we have done for potential energy function and first derivative of q is quadratic in this equation and the lowest lowest nonvanishing approximation to T is obtained by retaining only the firt term in the Taylor series expansion of m(q) which is m(0). Thus Lagrangian for small oscillations of one dimensional oscillator is

and equation of motion is

Stable and unstable equilibrium

First consider the figures given below

• Above are the plots of potential energy as a function of x , for a particle executing bound and unbound motion.
• At x₀=0 slope of potential energy curve dV/dx is zero. this implies that F = 0 i.e.,
          F = -dV/dx = 0                 (1)
  and a point particle placed at such a point with zero velocity will continue to remain at rest.
• At point x₀ in figugure (a) at which potential energy has a minimum , if the particle is displaced then the force F = -dV/dx will tend to return to it and it will oscillate about the equilibrium point, performing bound motion. These points are called points of stable equilibrium.
• If the particle is displaced slightly from the equilibrium x₀ in figure (b) , then it will be acted upon by the force
        F(x) = -(-dV/dx) = dV/dx          (2)
  which will tend to push away the particle from equilibrium point , when released. Such points are called points of unstable equilibrium.

Potential energy about point of stable equilibrium
Suppose the particle is slightly displaced from point of stable equilibrium executing small oscillations then potential energy function can be expressed in the form of Taylor - series expansion i.e.,

Hamiltonian formulism of mechanics (part 2)

-Following four forms of generator are possible : F₁(q,Q,t) , F₂(q,P,t) , F₃(p,Q,t) , F₄(p,P,t)

  Legendre transforms are
    g(u,y)=f(x,y)-ux
    where u=(∂ F/∂ x)
 (i) F₁=F₁(q,Q,t) putting it in equation 1 and finding derivative of F w.r.t. we get
          p_j = ∂F₁(q,Q,t)/∂q_j

          P_j = - ∂F₁(q,Q,t)/∂Q_j

          K=H+∂F₁(q,Q,t)/∂t
(ii) putting u = -P_j , x = Q_j , y = q_j , g = F₂(q,P,t) , f=F₁ and using Legender transforms we get
          F₂(q_j,P_j,t) = F₁(q_j,Q_j,t)+ΣP_jQ_j
         Putting this in 1 and solving we get
          p_j = ∂F₂(q_j,P_j,t)/∂q_j

          Q_j =  ∂F₂(q_j,P_j,t)/∂P_j

          K=H+∂F₂(q_j,P_j,t)/∂t

 (iii) F₃ = F₃(Q,p,t) is the third form
            Connect it to the first form using legender transforms
            Since p_j = ∂F₁(q_j,P_j,t)/∂q_j and u=∂f/∂x
             this implies that u=p_j , x=q_j , y=Q_j , g=F₃ , f=F₁
              Thus,  F₃ = F₁(Q,q,t)-Σp_jq_j
              or, F₁(Q,q,t)=F₃+Σp_jq_j
              putting these in equation 1
            q_j = -∂F₃(p_j,Q_j,t)/∂p_j
            P_j = -∂F₃(p_j,Q_j,t)/∂Q_j

             K=H+∂F₃(p_j,Q_j,t)/∂t
(iv)    Fourth form is F₄(p,P,t) , connecting F₄ by F₁ through legender transforms and solving we get
         q_j = -∂F₄(p_j,P_j,t)/∂p_j

         Q_j = ∂F₄(p_j,P_j,t)/∂P_j
         K=H+∂F₄(p_j,P_j,t)/∂t

Hamiltonian Formulism of mechanics (part 1)

Hamiltonian is H=T+V
or,

Hamilton's Canonical Equations of motion:-

• Co-ordinates cyclic in Lagrangian will also be cyclic in Hamiltonian.
• Canonical transformations are characterized by the property that they leave the form of Hamilton's equations of motion invarient.
• Lagrange's equation of motion are covarient w.r.t. point transformations (Q_j=Q_j(q_j,t) and if we define P_j as,
  

         

     

           the Hamilton's canonical equation will also be covarient.

• Consider the transformations
  
         Q_j=Q_j(p,q,t)
         P_j=P_j(p,q,t)
         where Q_j and P_j are new set of co-ordinates.
• For Q_j and P_j to be canonical they should be able to be expressed in Hamiltonian form of equations of motion i.e.,
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
   where,  K=K(Q,P,t) and is substitute of Hamiltonian H of old set in new set of co-ordinates.
• Q_j and P_j to be canonical must also satisfy modified Hamilton's principle i.e.,
  
  
  
  
  
  
  
  
  
  
  
  
  
  
• Using same principle for old set q_j and p_j
  
                             (1)
  
  
   where F is any function of phase space co-ordinates with continous second derivative.
• Term ∂F/∂t in 1 contributes to the variation of the action integral only at end points and will therefore vanish if F is a function of (q,p,t) or (Q,P,t) or any mixture of phase space co-ordinates since they have zero variation at end points.
  
• F is useful for specifying the exact form of anonical transformations only when half of the variables (except time) are from the old set and half from the new set.
  
• F acts as bridge between two sets of canonical variables and is known as generating function of transformations.
  

In next post I'll discuss more about generating functions , lagrange and poisson brackett.

Constrains and constrained motion

• A constrained motion is a motion which can not proceed arbitrary in any manner.
• Particle motion can be restricted to occur (1) along some specified path (2) on surface (plane or curved) arbitrarily oriented in space.
• Imposing constraints on a mechanical system is done to simplify the mathematical description of the system.
• Constraints expressed in the form of equation f(x₁,y₁,z₁,......,x_n,y_n,z_n :t)=0 are called holonomic constraints.
• Constraints not expressed in this fashion are called non-holonomic constraints.
• Scleronomic conatraints are independent of time.
• Constraints containing time explicitely are called rehonomic.
• Therefore a constraint is either

          "Scleronomic where constraints relations does not depend on time or rheonomic where constraints relations depends explicitly on time "
          and either
           "holonomic where constraints relations can be made independent of velocity or non-holonomic where these relations are irreducible functions of velocity"

Constraints types of some physicsl systems are given below in the table